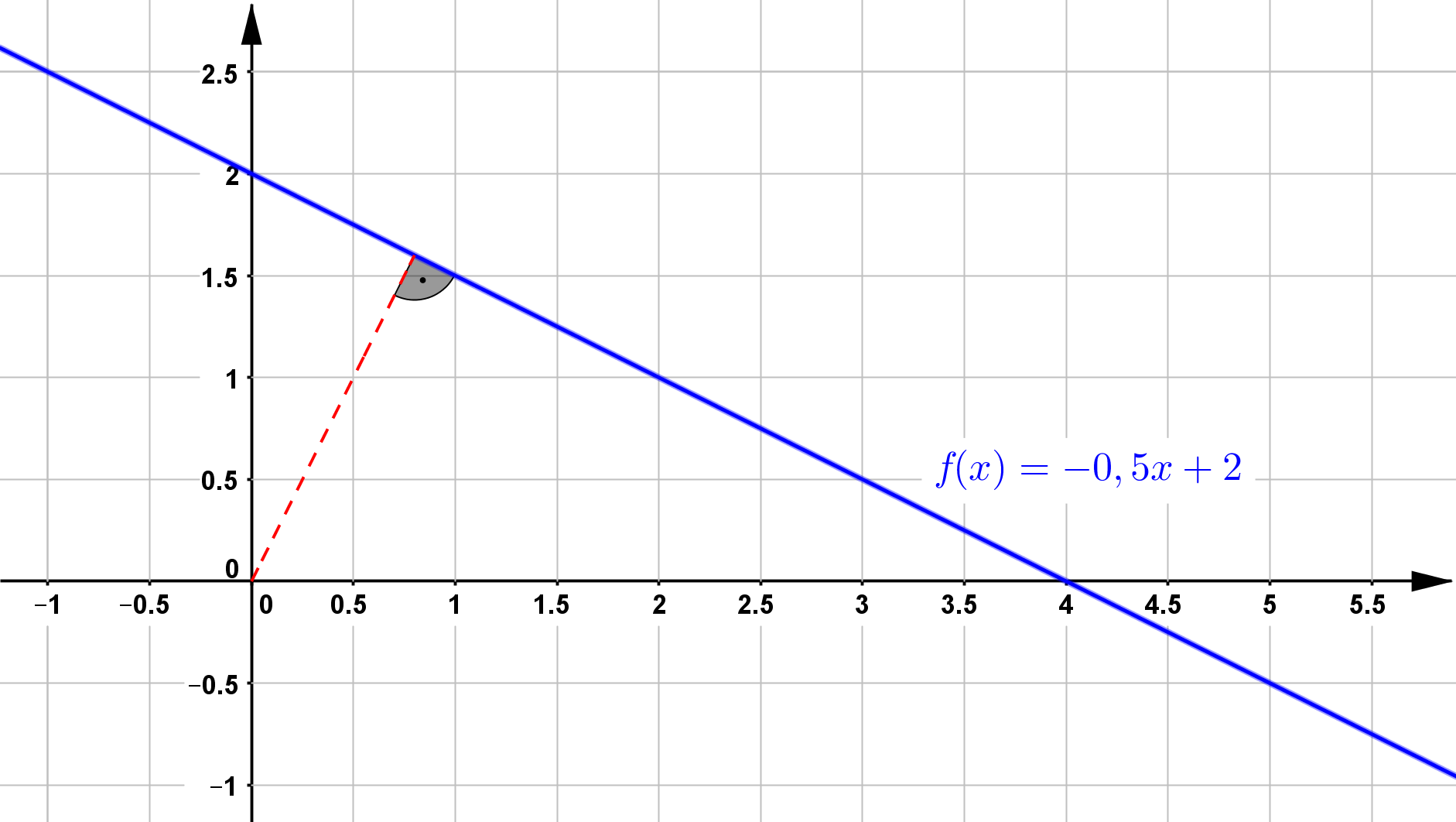
In vielen Anwendungen und Fragestellungen ist es notwendig, die zu einer bekannten Geraden senkrechte Richtung zu kennen. Bei der Frage nach dem
Abstand einer Geraden von bestimmten Punkten etwa ist die Linie, die den Abstand darstellt, senkrecht zu der Geraden. Wenn man nun die
Steigung der Linie (Geraden), auf der der Abstand bestimmt wird, kennt, kann mit Hilfe des gegebenen Punktes und der Punkt-Steigungs-Form
eine Funktion gefunden werden. Der Schnittpunkt der gegebenen Funktion mit der eben gefundenen Funktion ergibt dann zusammen mit dem
gegebenen Punkt die Möglichkeit, den Abstand zu bestimmen. Klingt erstmal kompliziert, ist aber ganz einfach...
Für die Ermittlung der senkrechten Richtung kann eine Darstellung einer Geraden mit eingezeichnetem Steigungsdreieck helfen. Die Gerade und das
Steigungsdreieck werden um 90° im Uhrzeigersinn gedreht. Das entstandenen grüne Steigungsdreick hat die Werte $\Delta y = 1$ und $\Delta x = 0,5$.
Damit errechnet sich die Steigung der gedrehten Funktion zu $m_\bot = 2$.
Allgemein lautet die Steigung $m_1$ senkrecht zur Steigung $m_2$: $$ \mathbf{m_1 = - \frac{1}{m_2}} $$
Es soll der Abstand zwischen der Funktion $f(x)$ und dem Koordinatenursprung bestimmt werden. Damit soll die gesuchte Funktion, z.B. $g(x)$, durch den Punkt $P (0/0)$ verlaufen. Mit der Punkt-Steigungs-Form einer linearen Funktion lässt sich der Funktionsterm für $g(x)$ bestimmen: \begin{align} \left( y - y_1 \right) &= m \cdot \left( x - x_1 \right) \qquad \qquad \text{mit:} \, x_1 = 0 \text{ und} \; y_1 = 0 \\ y &= 2 \cdot x \end{align} Also: $ g(x) = 2 x$.
Es gilt $f(x) = g(x)$ für die Bestimmung des Schnittpunkts:
\begin{align}
f(x) &= g(x) \\
- 0,5 x + 2 &= 2 x \\
2 &= 2,5 x \\
x &= \frac{4}{5} = 0,8
\end{align}
Der $x$-Wert wird in eine der beiden Funktionen eingesetzt: $g(x) = 2 \cdot 0,8 = 1,6$
$$
S (0,8 / 1,6)
$$
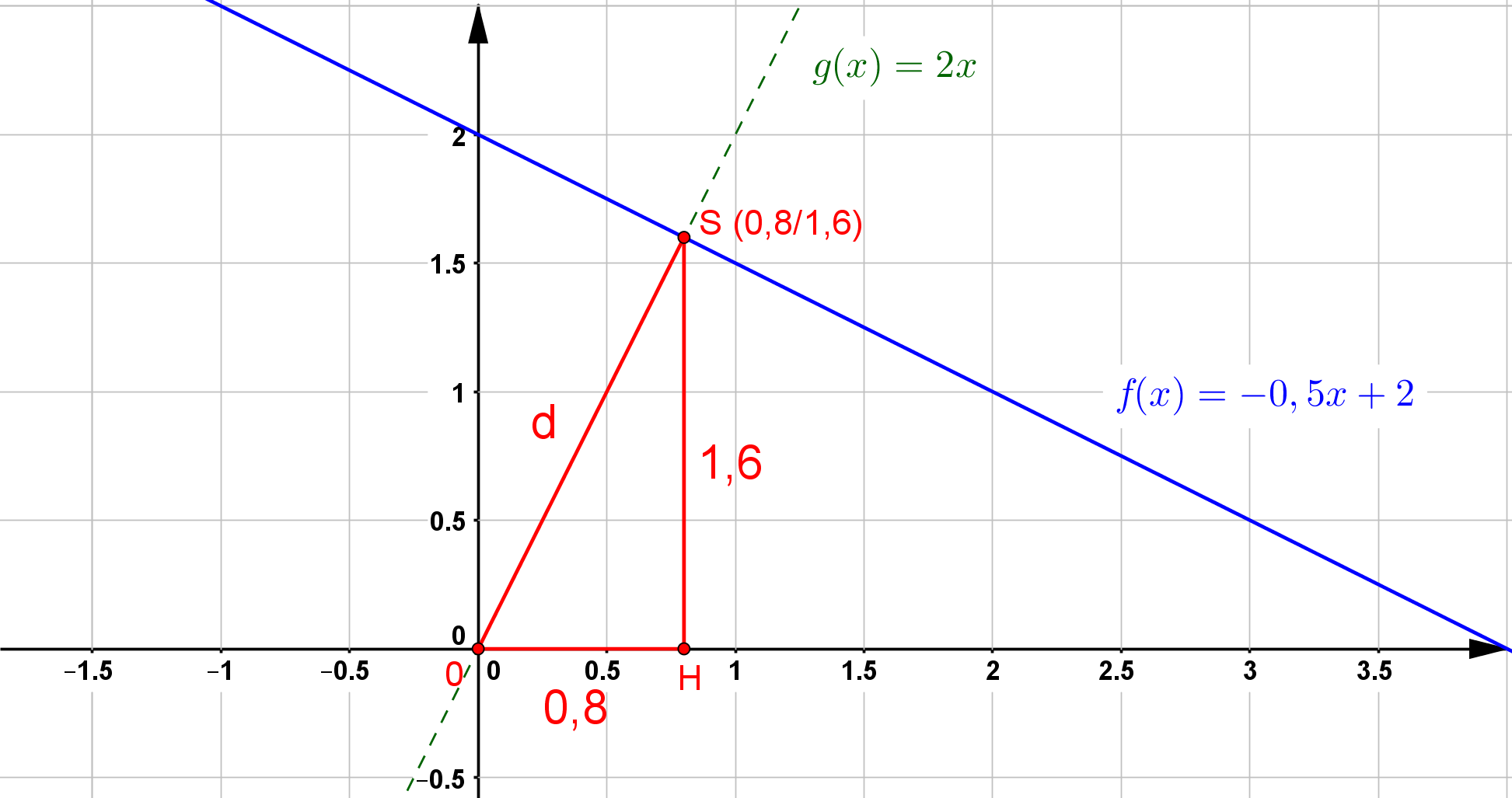Für die Abstandsbestimmung wird der Satz des Pythagoras genutzt. Es folgt:
\begin{align}
d &= \sqrt{1,6^2 + 0,8^2} \\
d &= 1,79
\end{align}
© mondbrand MMXIX